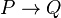Rabu, 04 Mei 2011

Inverse (Logic)

The inverse is a type of conditional sentence in formal logic. Any conditional sentence has an inverse: the contrapositive of the converse. The inverse of P \rightarrow Q is thus 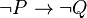\neg P \rightarrow \neg Q . For example, substituting propositions in natural language for logical variables, the inverse of the conditional proposition "If it's raining, then Sam will meet Jack at the movies." is "If it's not raining, then Sam will not meet Jack at the movies.".
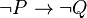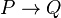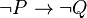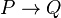The inverse of the inverse, that is, the inverse of \neg P \rightarrow \neg Q , is \neg \neg P \rightarrow \neg \neg Q . Since a double negation has no logical effect, the inverse of the inverse is logically equivalent to the original conditional P \rightarrow Q . Thus it is permissible to say that \neg P \rightarrow \neg Q and P \rightarrow Q are inverses of each other. Likewise, we may say that 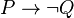P \rightarrow \neg Q and \neg P \rightarrow Q are inverses of each other.
The inverse and the converse of a conditional are logically equivalent to each other, just as the conditional and its contrapositive are logically equivalent to each other. But the inverse of a conditional is not inferable from the conditional. For example, "If it's not raining, then Sam will not meet Jack at the movies." cannot be inferred from "If it's raining, then Sam will meet Jack at the movies.". It could easily be the case that Sam and Jack are attending the movies no matter the weather.
Diposting oleh di Tidak ada komentar:
Langganan: Postingan (Atom)